粮食市场机制分析：产量与价格的互动
汤 亮
中国社会科学院数量经济与技术经济研究所 博士后
摘要：本文利用去除灾害影响后的产量与单产数据，研究了粮食产量与价格之间的互动关系。通过实证检验，发现粮食市场中确实存在蛛网模型的动态机制，同时也受到货币发行量变化的重大影响。另外，粮食生产者也能够对真实粮食几个变化做出合理的反应。因此，在政策上保证粮食价格的比较优势、维持货币发行的稳定以及提升粮食生产应对自然灾害的能力有助于促进粮食安全和市场稳定。
关键词：粮食安全、粮食市场、粮食价格、蛛网模型
Abstract：This paper studies the dynamic inter-relationship between grain product and its price through with the corrected data which removed the impacts of natural calamities. The empirical results show that there exists a cobweb dynamic mechanism in the market, and price of grain is also influenced by the variation of money issuing. At the meantime, the farmers can response to the change of real price reasonably. Therefore, it is vital for government to maintain the advantage of grain price to other industries, to keep a smooth money supply, and to improve the capability of anti-calamity in agriculture.
Key words: food security, grain market, grain price, cobweb model
粮食安全是我国始终面临的重要问题。确保一定水平的粮食产量和国内保障能力，对我国实现经济快速发展和社会长期稳定至关重要。同时，维持粮食价格的基本稳定也是国家宏观调控的重要方面。2003年以来，我国实现了连续9年粮食增长，创造了持续增长的历史纪录。但是粮食价格一直波动较大，为宏观经济调控尤其是通货膨胀的控制带来新的挑战。本文将对粮食产量与价格之间的互动关系进行实证分析研究，为有关决策提供参考并提出政策建议。
一、文献综述
对粮食增产尤其是单产增加的研究可以分为两个方面：技术因素和市场因素。技术因素主要集中在化肥、机械化水平、农业技术等对产量增长的贡献上；而市场因素主要集中在粮食产量与粮食价格尤其是收购价格的关系上。
对我国粮食生产和价格波动问题，国内学者做了大量的研究。张治华（1997）通过对粮食生产和价格之间的周期性变化分析，认为价格对我国粮食生产起着明显的调节和促进作用，同时粮食产量也引起价格的变动。由于粮食供给价格弹性比粮食需求价格弹性大，因而粮食价格对供给调节相对容易，对需求调节则比较困难。
蒋乃华（1998）认为，粮食生产的波动是引起价格波动的最基本因素，而价格杠杆对调节农户的粮食生产行为有着至关重要的作用。孙娅范等（1999）应用Granger因果关系检验和时间序列分析，也得出类似的结论,即粮食价格与粮食产量存在因果关系，粮食收购价格对粮食产量的影响要大于对粮食市场零售价格的影响。
占绍文等（2008）利用1950-2007年中国农业生产统计数据，运用C-D函数和珠网理论分析我国粮食价格波动对其播种面积的影响，能够得出结论：粮食价格上涨对农民增加种植面积、增加农业生产投入有显著影响。
粮食生产中面临的价格，不仅是粮食收购价格，它还要面临上游价格。也就是说，农民需要考虑成本效益两个方面。因此，本文从总体数据角度，首先对蛛网模型的两个重要关系——粮食产量对价格的影响，和价格对粮食产量的影响进行实证检验，然后本文将分析粮食真实价格——粮食与工业品比价——的变化与粮食生产的关系，从而分析农民是否能够对市场变化做出主动反应。
二、粮食产量影响因素与数据
对粮食市场的实证分析首先应该去除意外波动的影响。这种意外波动主要来自自然灾害。由于自然灾害在发生频率、发生强度上有较大差异，所以会导致粮食产量数据的较大波动。要进行数据分析，就需要去除这种外生的波动。
粮食产量的决定因素主要有四个方面：粮食播种面积，化肥施用量，技术条件如农业机械化水平、良种推广水平等，自然灾害的影响。在数据分析中，技术条件在短期内没有大的变化，尤其是在总体数据上看更是如此；水利设施、降水等因素可以考虑在自然灾害的影响之中。因此，通过对粮食产量与粮食播种面积、化肥施用量、成灾面积的关系既可以分析技术条件没有较大变化时的粮食产量影响因素。
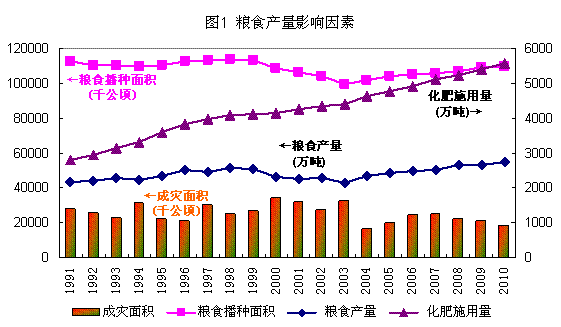数据来源：国家统计局，《中国统计年鉴》，2011。
从图1可以看出，粮食播种面积成灾面积两个变量的波动比较大；而化肥施用量基本上是一个不断上升的趋势，但是在不同年份的变化率差异较大；粮食产量曲线也有波动，但是幅度小于播种面积和成灾面积。变量之间的回归结果见表1。
表1 粮食产量贡献因素分析
|
应变量： 粮食产量 |
||||
|
Sample：1991—2010 |
||||
|
自变量 |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
粮食播种面积 |
0.591 |
0.04 |
14.78 |
0.0000 |
|
化肥施用量 |
4.038 |
0.22 |
18.59 |
0.0000 |
|
成灾面积 |
-0.141 |
0.032 |
-4.45 |
0.0004 |
|
C |
-29333.86 |
5077.24 |
-5.78 |
0.0000 |
|
R-squared |
0.97 |
Akaike info criterion |
15.88 |
|
|
Adjusted R-squared |
0.97 |
F-statistic |
186.75 |
|
|
Durbin-Watson stat |
1.87 |
Prob(F-statistic) |
0.000000 |
|
除掉灾害因素，重估如果没有灾害影响应该得到的粮食产量：
校正粮食产量= 0.591*种植面积 + 4.038*化肥使用量-29333.86
同时，利用粮食播种面积去除校正后的粮食产量，可以得到校正后的粮食单产水平。校正后的粮食产量和单产数据以及化肥施用数据见表2。
表2 粮食产量校正
|
年份 |
粮食产量 （万吨） |
校正产量 （万吨） |
粮食单产 （吨/公顷） |
校正后单产 （吨/公顷） |
化肥总平均施用量 （吨/公顷） |
化肥总平均施用量 （公斤/亩） |
|
1991 |
43529 |
48349.35 |
3.876 |
4.305 |
0.250 |
16.65 |
|
1992 |
44266 |
47818.2 |
4.004 |
4.325 |
0.265 |
17.67 |
|
1993 |
45649 |
48683.25 |
4.131 |
4.405 |
0.285 |
19.01 |
|
1994 |
44510 |
48783.4 |
4.063 |
4.453 |
0.303 |
20.19 |
|
1995 |
46662 |
50201.89 |
4.240 |
4.561 |
0.327 |
21.77 |
|
1996 |
50454 |
52617.5 |
4.483 |
4.675 |
0.340 |
22.67 |
|
1997 |
49417 |
53449.54 |
4.377 |
4.734 |
0.353 |
23.50 |
|
1998 |
51230 |
54382.4 |
4.502 |
4.779 |
0.359 |
23.93 |
|
1999 |
50838.6 |
54176.48 |
4.493 |
4.788 |
0.364 |
24.30 |
|
2000 |
46217.5 |
51490.07 |
4.261 |
4.747 |
0.382 |
25.49 |
|
2001 |
45263.7 |
50515.83 |
4.267 |
4.762 |
0.401 |
26.73 |
|
2002 |
45705.8 |
49568.05 |
4.399 |
4.771 |
0.418 |
27.85 |
|
2003 |
43069.53 |
47212.49 |
4.333 |
4.749 |
0.444 |
29.59 |
|
2004 |
46946.95 |
49418.15 |
4.620 |
4.864 |
0.456 |
30.42 |
|
2005 |
48402.19 |
51520.46 |
4.642 |
4.941 |
0.457 |
30.47 |
|
2006 |
49804.23 |
52574 |
4.745 |
5.009 |
0.469 |
31.30 |
|
2007 |
50160.28 |
53703.34 |
4.748 |
5.084 |
0.484 |
32.23 |
|
2008 |
52870.92 |
54915.03 |
4.951 |
5.142 |
0.491 |
32.71 |
|
2009 |
53082.08 |
56878.51 |
4.871 |
5.219 |
0.496 |
33.06 |
|
2010 |
54647.71 |
58039.61 |
4.974 |
5.282 |
0.506 |
33.75 |
注：校正后单产数字为估计值。化肥施用量高于实际数值，因为统计数据中化肥不只使用与粮食生产，还用于蔬菜、果木等的生产。
数据来源：国家统计局，《中国统计年鉴》，2011。
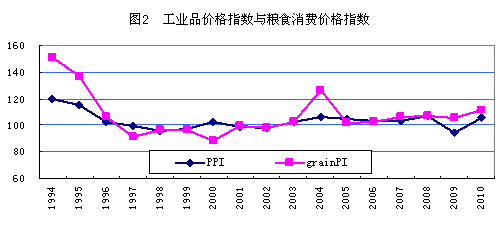
在价格数据中，本文采用历年统计年鉴提供的居民消费价格分类指数中的粮食价格指数（如2011年《中国统计年鉴》的表9-6）与工业品出厂价格指数（2011年《中国统计年鉴》的表9-11），转化为年度变化率后以二者之差作为粮食真实价格的变化率。
三、实证分析
（一）对蛛网模型的检验
在对农业产品供给与需求的分析中，一般都认为农产品价格与产量之间存在着蛛网型动态关系。在蛛网模型中，供给量取决于上期价格水平，同时下一期的价格水平又受本期产量的影响。因此，供给量就会表现出对价格变化的追赶，最终形成一种价格与供给量的循环。
通过对校正后粮食产量变化率与滞后一期的粮食价格变化率的回归（表3），可以看出,二者确实有较好的拟合。在统计意义上可以证明，存在粮食价格对下一期校正后产量的先导关系。同时，从表4可以看出，使用校正后粮食产量的变化率确实具有比未校正的粮食产量变化率更好的统计学特征。使用未校正数据，在5%的统计水平上不能证明这种先导关系。这是因为，数据校正排除了自然灾害对粮食产量的影响。
表3 校正后产量变化率对滞后一期粮价变化率的回归
|
应变量： 校正后粮食产量变化率 |
||||
|
样本期（调整后）： 1995—2010 |
||||
|
自变量 |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
粮食价格变化率(-1) |
0.0997 |
0.0414 |
2.409 |
0.0304 |
|
C |
0.0041 |
0.00734 |
0.557 |
0.586 |
|
R-squared |
0.293 |
Akaike info criterion |
-4.288 |
|
|
Adjusted R-squared |
0.243 |
F-statistic |
5.802 |
|
|
Durbin-Watson stat |
1.588 |
Prob(F-statistic) |
0.0304 |
|
表4 未校正产量变化率对滞后一期粮价变化率的回归
|
应变量： 粮食产量变化率 |
||||
|
样本期（调整后）： 1995—2010 |
||||
|
自变量 |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
粮食价格变化率(-1) |
0.134 |
0.0667 |
2.011 |
0.064 |
|
C |
0.00417 |
0.0118 |
0.353 |
0.73 |
|
R-squared |
0.224 |
Akaike info criterion |
-3.33 |
|
|
Adjusted R-squared |
0.169 |
F-statistic |
4.043 |
|
|
Durbin-Watson stat |
2.64 |
Prob(F-statistic) |
0.064 |
|
在验证了粮价对产量的先导关系之后，还需要验证蛛网模型的另一方面，即实际产量对下一期粮食价格的影响。通过回归分析（表5）可以看出，这种关系在统计学意义上也确实存在。同时粮食价格变化率也受前一期变化率的显著影响。粮食产量1%的增加，将会引起下一期粮食价格下跌1.4个百分点。同时，前一期粮食价格的波动，将会有约56%传递过来。这种机制背后是货币等因素的影响，价格变动的传导不仅局限于一期，而是会影响多期。
表5 从滞后一期粮价变化率到实际产量对变化率的回归
|
应变量： 粮食价格变化率 |
||||
|
样本期（调整后）： 1995—2010 |
||||
|
自变量 |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
粮食价格变化率(-1) |
0.562 |
0.129 |
4.356 |
0.0008 |
|
粮食产量变化率(-1) |
-1.395 |
0.448 |
-3.113 |
0.0082 |
|
C |
0.022 |
0.022 |
1.028 |
0.3229 |
|
R-squared |
0.633 |
Akaike info criterion |
-2.066 |
|
|
Adjusted
R-squared |
0.576 |
F-statistic |
11.194 |
|
|
Durbin-Watson
stat |
1.344 |
Prob(F-statistic) |
0.00149 |
|
但是，表5中的回归结果仍然存在一个问题，那就是其常数项的标准差太大，显示这一模型仍有需要的变量没有考虑进来。这一变量就是货币发行。事实上，如果供求关系没有发生大的变化，任何商品和资产的价格都是货币现象。对粮食价格尤其如此，因为其需求基本保持稳定。选取M2变化率作为新的自变量重新模拟，就得出了一个在各个统计指标上都非常优良的回归结果（表6）
表6 包含了货币因素的粮价决定模型
|
应变量： 粮食价格变化率 |
||||
|
样本期（调整后）： 1995—2010 |
||||
|
自变量 |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
粮食产量变化率(-1) |
-1.226 |
0.494 |
-2.481 |
0.0276 |
|
货币发行（M2）变化率 |
1.695 |
0.482 |
3.516 |
0.0038 |
|
C |
-0.252 |
0.091 |
-2.775 |
0.0158 |
|
R-squared |
0.537 |
Akaike info criterion |
-1.835 |
|
|
Adjusted R-squared |
0.466 |
F-statistic |
7.534 |
|
|
Durbin-Watson stat |
1.463 |
Prob(F-statistic) |
0.0067 |
|
表6的回归结果表明，如果直接以货币变化来代替上期价格的影响，模型结果更为合理。上期粮食产量的负面影响仍然较大，1个百分点的产量增长会带来下期约1.2%的下跌；而当期货币影响更大，如果M2发行量增发1个百分点，将带来当期粮价1.7%的百分点的上涨。从现实市场的经验看，这两个结果都是比较吻合的。
从以上分析可以看出，粮食市场中确实存在这蛛网模型的运转机制。首先，前一期的粮食价格走势会影响到下一期粮食供给的积极性，粮价上涨，供给意愿增加。如果没有自然灾害的意外影响，供给会趋于增加。其次，今年的粮食实际产量增长，会影响第二年的粮食价格，如果排除掉其他因素如货币供应量、收购价政策、补贴等的变化，前期产量增加，后期的价格就会下降。
（二）适应性预期还是理性预期？
蛛网模型的隐含机制是生产者的适应性预期形式，即认为上一期的价格会成为本期的价格，或者会以一定比例进入本期。因此生产者会按上期的价格来推测本期的效益水平并决定当期的预期生产量。然后，这种预期生产量在合并了本期发生的各种事件包括自然灾害等形成了本期的实际生产量，之后又参与下一期价格的形成。尽管在统计意义上存在粮价与产量（校正后）的动态互动关系，但是这并不代表农民只能受蛛网型循环走势的影响。实际损失，农民能够对各方面信息进行综合，调整自己的生产行为。
为分析粮食生产者的行为，对校正后的粮食产量和单产的变化与真实粮食价格——去除工业品价格变化因素后的粮食价格变动进行回归。通过计量分析可以看出，校正后粮食产量、校正后粮食单产与滞后一期的粮食真实价格变化的关系在统计上的显著性反而不如对当期价格变化（表7、8、9、10）。在这里，真实粮食价格变化等于粮食价格指数减去工业品出厂价格指数，再除以100转化为变化率。
表7 校正后粮食产量与真实价格变化的回归结果
|
应变量： 校正后粮食产量变化率 |
||||
|
样本期（调整后）： 1996—2010 |
||||
|
自变量 |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
真实粮价变化率 |
0.236 |
0.0792 |
2.984 |
0.0124 |
|
真实粮价变化率(-1) |
0.146 |
0.0754 |
1.942 |
0.0782 |
|
C |
0.00498 |
0.00809 |
0.615 |
0.551 |
|
AR(1) |
0.2512 |
0.232719 |
1.079262 |
0.304 |
|
R-squared |
0.587 |
Akaike info criterion |
-4.501 |
|
|
Adjusted R-squared |
0.474 |
F-statistic |
5.205 |
|
|
Durbin-Watson stat |
1.070 |
Prob(F-statistic) |
0.0176 |
|
|
Inverted AR Roots |
.25 |
|||
表8 校正后粮食产量与真实价格变化的回归结果（2）
|
应变量： 校正后粮食产量变化率 |
||||
|
样本期（调整后）： 1995—2010 |
||||
|
自变量 |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
真实粮价变化率 |
0.182 |
0.075 |
2.423 |
0.0296 |
|
C |
0.007 |
0.007 |
0.956 |
0.355 |
|
R-squared |
0.295 |
Akaike info criterion |
-4.292 |
|
|
Adjusted R-squared |
0.245 |
F-statistic |
5.869 |
|
|
Durbin-Watson stat |
1.043 |
Prob(F-statistic) |
0.030 |
|
表9 校正后粮食单产与真实价格变化的回归结果
|
应变量： 校正后粮食单产变化率 |
||||
|
样本期（调整后）： 1996—2010 |
||||
|
自变量 |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
真实粮价变化率 |
0.074 |
0.023 |
3.234 |
0.008 |
|
真实粮价变化率(-1) |
0.031 |
0.022 |
1.417 |
0.184 |
|
C |
0.008 |
0.003 |
3.196 |
0.009 |
|
AR(1) |
0.339 |
0.280 |
1.212 |
0.251 |
|
R-squared |
0.619 |
Akaike info criterion |
-6.973 |
|
|
Adjusted R-squared |
0.515 |
F-statistic |
5.950 |
|
|
Durbin-Watson stat |
1.045 |
Prob(F-statistic) |
0.0115 |
|
|
Inverted AR Roots |
.34 |
|||
表10 校正后粮食单产与真实价格变化的回归结果（2）
|
应变量： 校正后粮食单产变化率 |
||||
|
样本期（调整后）：1996—2010 |
||||
|
自变量 |
Coefficient |
Std. Error |
t-Statistic |
Prob. |
|
真实粮价变化率 |
0.061 |
0.020 |
3.053 |
0.010 |
|
AR(1) |
0.583 |
0.250 |
2.327 |
0.038 |
|
C |
0.009 |
0.004 |
2.147 |
0.053 |
|
R-squared |
0.581 |
Akaike info criterion |
-7.011 |
|
|
Adjusted R-squared |
0.511 |
F-statistic |
8.304 |
|
|
Durbin-Watson stat |
1.342 |
Prob(F-statistic) |
0.00545 |
|
|
Inverted AR Roots |
.58 |
|||
从以上回归结果可以看出，在生产决策上，农民能够综合考虑收购价格与投入品的价格。尤其是最能反映生产者增产意愿的校正后粮食单产对真实价格变化的回归，显示了良好的统计学特征。从这一点可以看出，农民具有一定程度的理性预期。
四、总结与政策讨论
本文利用计量经济方法去除灾害对产量的影响，对粮食价格与产量之间的相互关系进行了分析。结果表明，从总体数据的角度看，蛛网模型的动态互动机制确实存在。因此，如果外界条件不变，没有大的灾害或者政策变化，粮食市场将会呈现周期性的波动。同时，货币供给量的变化对粮食市场价格，从而对产量也将有很大影响。农民作为粮食生产者，不仅会受到历史价格的影响，而且能够对粮食真实价格的变化，即工农业产品比价的变化做出反应。
因此，为维持粮食安全和市场稳定，应该采取以下措施：第一，保持粮食价格稳定，并保持对工业品价格的一定比较优势。可以通过对粮食直补、对化肥、农用柴油等生产资料的补贴以及农业科技应用来提高粮食生产的真实效益。维持粮食价格稳定，对于保障国内粮食生产和供应具有重要意义；第二，保持货币供给的稳定，避免出现较大幅度的波动。因为货币供应对粮食价格波动具有较大的推动作用。一旦出现货币超量供应，将会引起粮食市场的剧烈波动；第三，加强农业基础设施建设，提高粮食生产应对自然灾害的能力。这有助于实现粮食市场的稳定。
参考文献
1、张治华，价格对我国粮食生产影响的实证分析及政策建议[J]。中国农村经济．1997（9）：11-18。
2、蒋乃华，价格因素对我国粮食生产影响的实证分析[J]。中国农村观察，1998（5）：14-20。
孙娅范，余海鹏．价格对中国粮食生产的因果关系及影响程度分析[J]。农业技术经济，1999 （2）：36-38。
3、占绍文、冯中朝、肖卫，浅析粮食价格变动对粮食播种面积的影响[J]内蒙古大学学报（哲学社会科学版），2008（5）：54-58。
4、何蒲明、黎东升、王雅鹏，粮食产量与价格波动的相互关系研究[J]。经济经纬（河南财经学院学报），2010 (1) 115～118。